중국 필수4는 문이과 공통으로 배우는 과목입니다.
여기 나온 공식(1/4)은 한국,일본 학생들도 알아야 하는 공식입니다.
삼각함수 공식은 많아서 쪼개서 올립니다.
(한꺼번에 모아서 올리니 난잡해 보이더라구요.)

$\displaystyle \sin \theta = \frac{y}{r}$
$\displaystyle \cos \theta = \frac{x}{r}$
$\displaystyle \tan \theta = \frac{y}{x}$
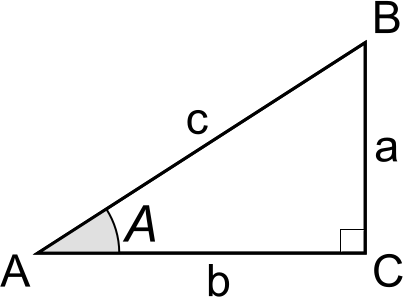
$\displaystyle \sin A = \frac{\mathrm{BC}}{\mathrm{AB}}$
$\displaystyle \cos A = \frac{\mathrm{AC}}{\mathrm{AB}}$
$\displaystyle \tan A = \frac{\mathrm{BC}}{\mathrm{AC}}$
$\displaystyle \sin^2 \theta + \cos^2 \theta =1$
$\displaystyle 1+\tan^2 \theta = \sec^2 \theta = \frac{1}{\cos^2 \theta}$
$\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}$

$\displaystyle a\sin\theta + b\cos\theta = \sqrt{a^2+b^2}\sin(\theta+\alpha)$
$\displaystyle \sin\alpha = \frac{b}{\sqrt{a^2+b^2}}$
$\displaystyle \cos\alpha = \frac{a}{\sqrt{a^2+b^2}}$

$\displaystyle \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$

$\displaystyle a^2 = b^2 + c^2 -2bc\cos A$
$\displaystyle b^2 = c^2+a^2-2ca\cos B$
$\displaystyle c^2 = a^2+b^2-2ab\cos C$
$\displaystyle \cos A = \frac{b^2+c^2-a^2}{2bc}$
$\displaystyle \cos B = \frac{c^2+a^2-b^2}{2ca}$
$\displaystyle \cos C = \frac{a^2+b^2-c^2}{2ab}$

$\displaystyle S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C$

$\displaystyle S = \sqrt{s(s-a)(s-b)(s-c)}\;\;,\:s = \frac{a+b+c}{2}$
이하 수학공식카드입니다.
퍼가는 거 막아놓지 않았으니, 다운로드 받아서 쓰세요.



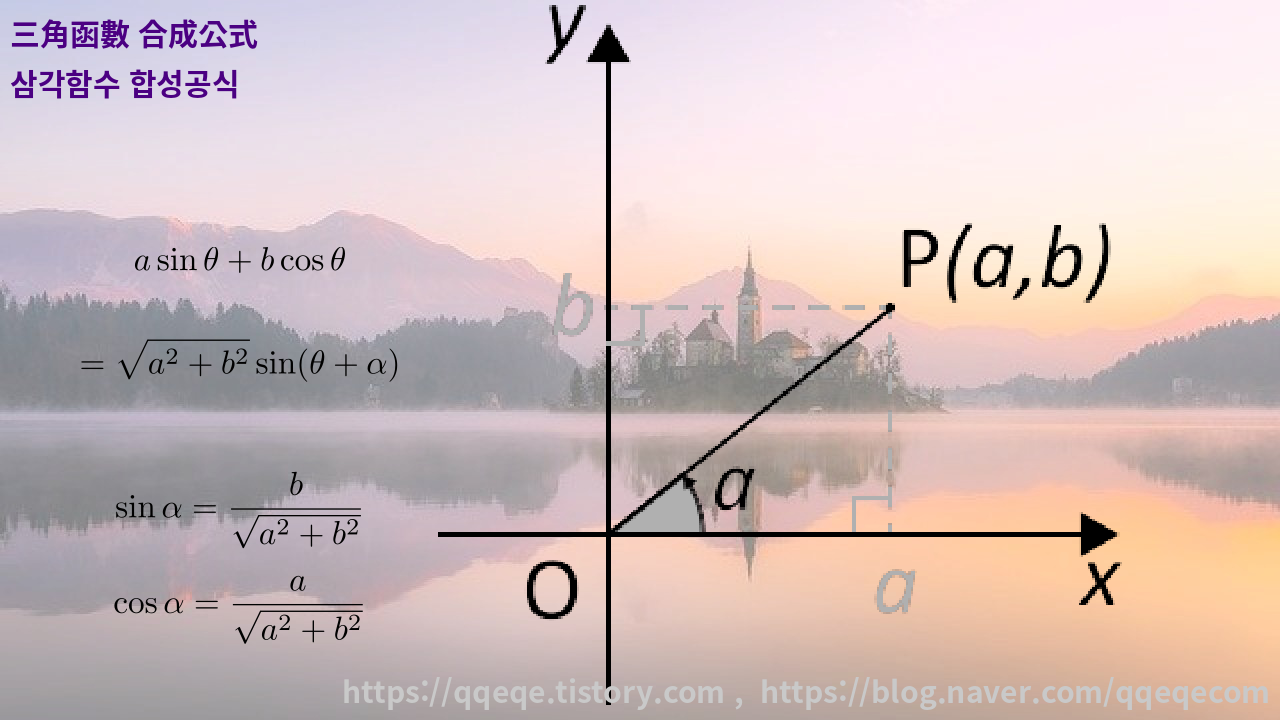

여기 나온 공식(1/4)은 한국,일본 학생들도 알아야 하는 공식입니다.
삼각함수 공식은 많아서 쪼개서 올립니다.
(한꺼번에 모아서 올리니 난잡해 보이더라구요.)
三角函數 삼각함수 정의

$\displaystyle \sin \theta = \frac{y}{r}$
$\displaystyle \cos \theta = \frac{x}{r}$
$\displaystyle \tan \theta = \frac{y}{x}$
三角比 삼각비

$\displaystyle \sin A = \frac{\mathrm{BC}}{\mathrm{AB}}$
$\displaystyle \cos A = \frac{\mathrm{AC}}{\mathrm{AB}}$
$\displaystyle \tan A = \frac{\mathrm{BC}}{\mathrm{AC}}$
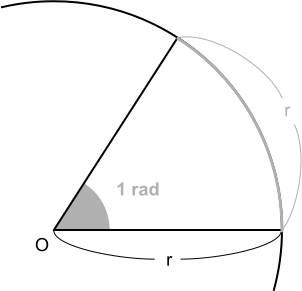
三角函數 基本公式 & 1rad
삼각함수 기본공식 & 라디안
$\displaystyle \sin^2 \theta + \cos^2 \theta =1$
$\displaystyle 1+\tan^2 \theta = \sec^2 \theta = \frac{1}{\cos^2 \theta}$
$\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta}$
三角函數 合成公式 삼각함수 합성공식

$\displaystyle a\sin\theta + b\cos\theta = \sqrt{a^2+b^2}\sin(\theta+\alpha)$
$\displaystyle \sin\alpha = \frac{b}{\sqrt{a^2+b^2}}$
$\displaystyle \cos\alpha = \frac{a}{\sqrt{a^2+b^2}}$
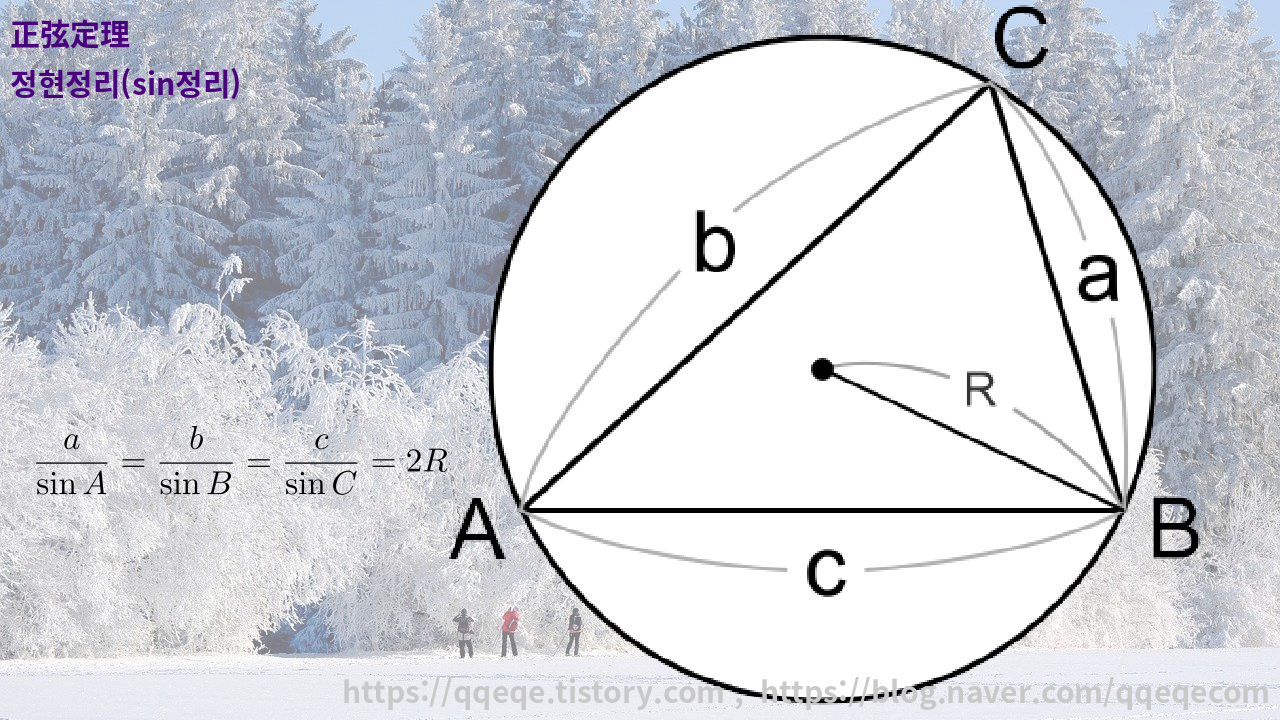
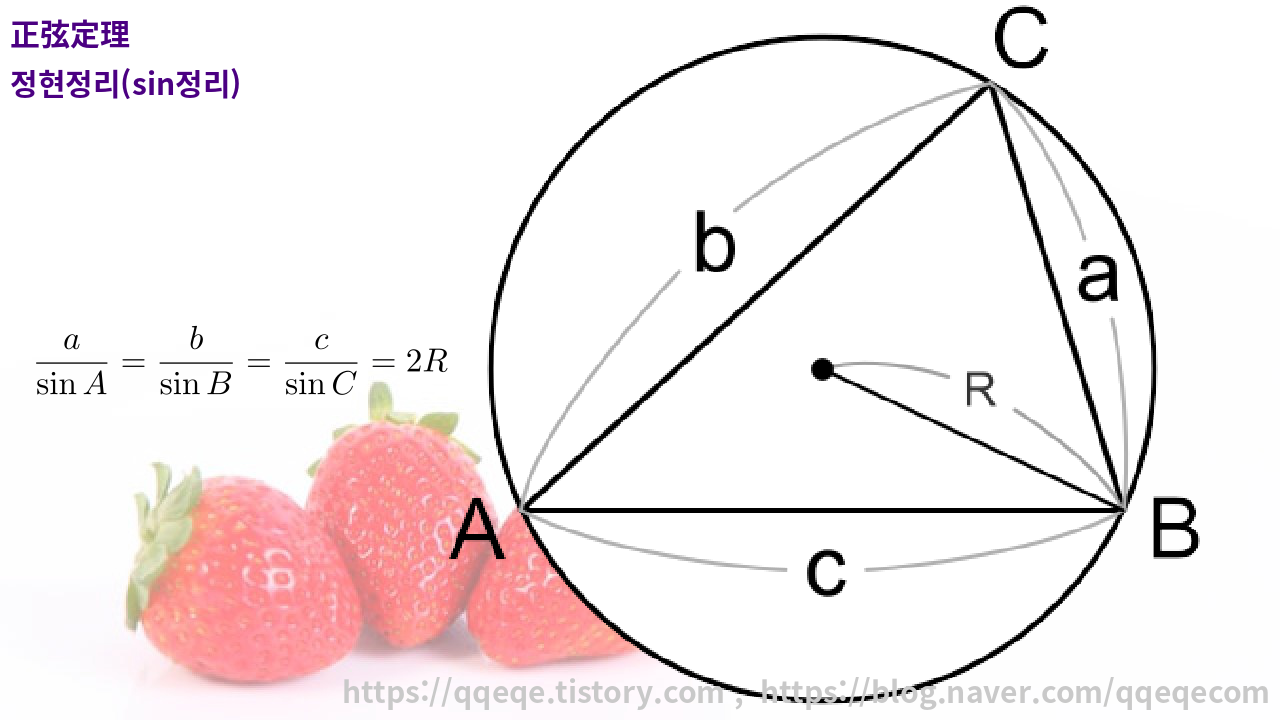
正弦定理 정현정리(sin정리)

$\displaystyle \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$
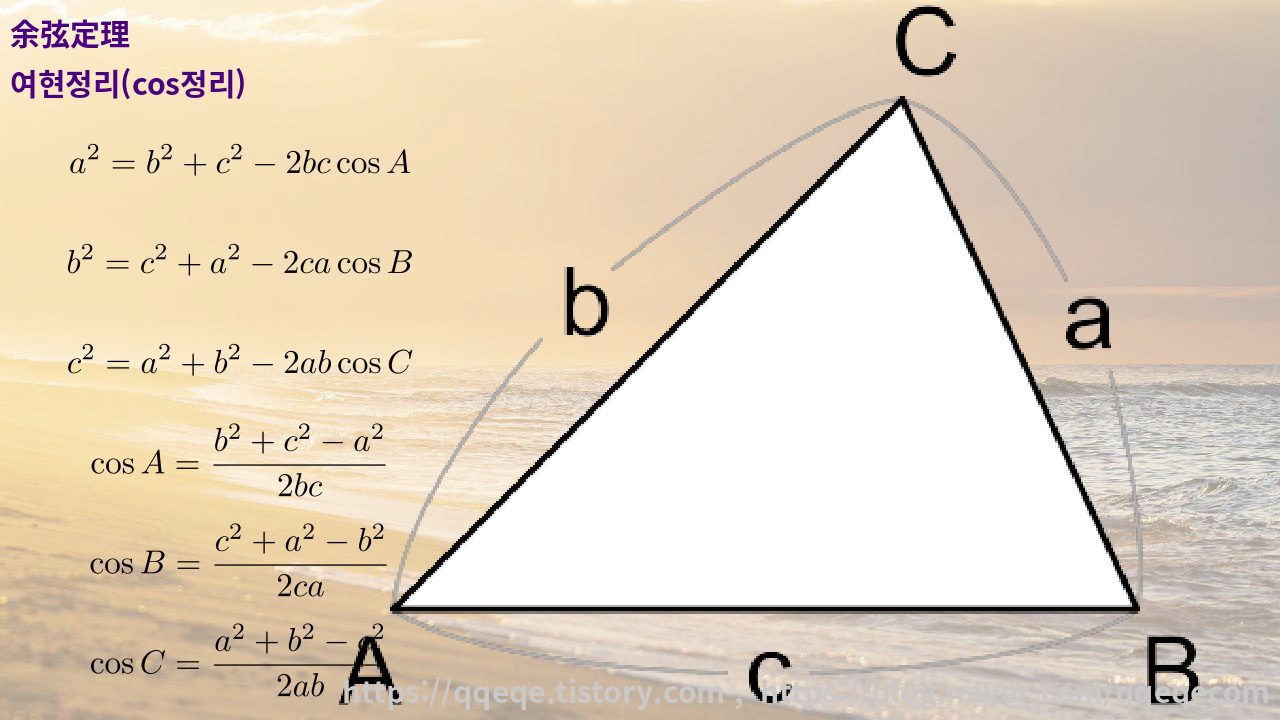
余弦定理 여현정리(cos정리)

$\displaystyle a^2 = b^2 + c^2 -2bc\cos A$
$\displaystyle b^2 = c^2+a^2-2ca\cos B$
$\displaystyle c^2 = a^2+b^2-2ab\cos C$
$\displaystyle \cos A = \frac{b^2+c^2-a^2}{2bc}$
$\displaystyle \cos B = \frac{c^2+a^2-b^2}{2ca}$
$\displaystyle \cos C = \frac{a^2+b^2-c^2}{2ab}$
面积公式 면적공식

$\displaystyle S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C$
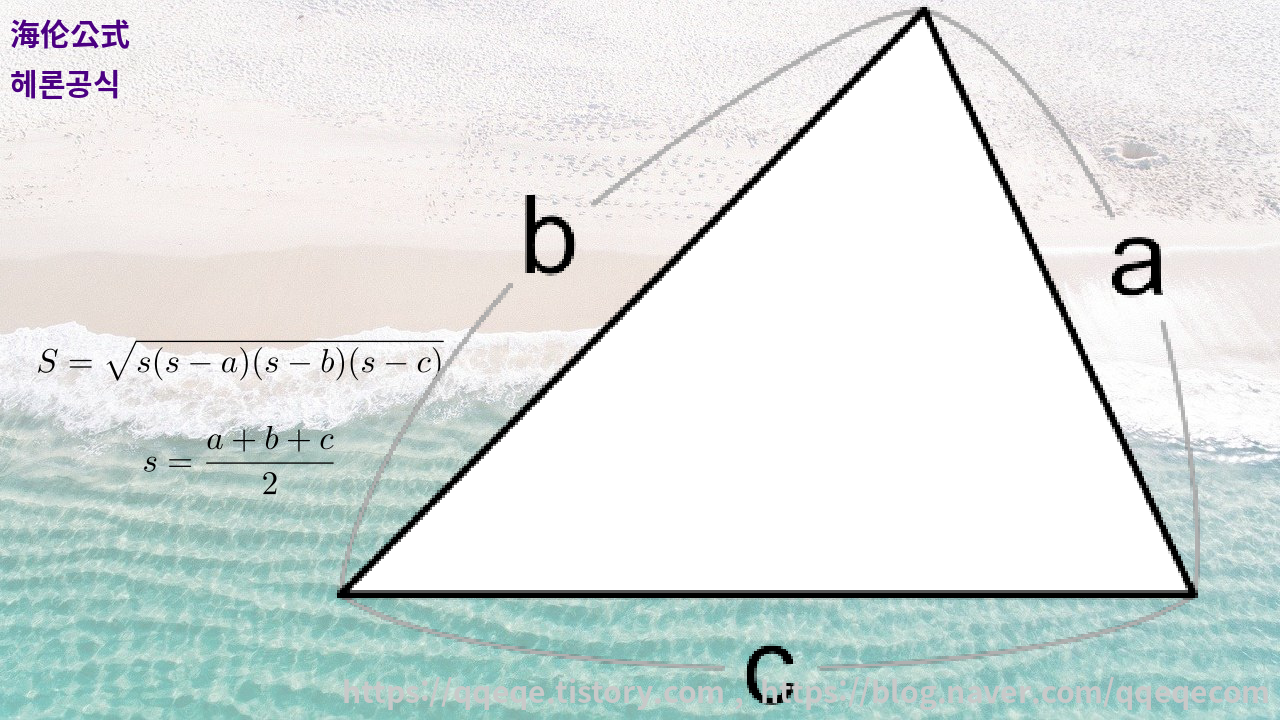
海伦公式 헤론공식

$\displaystyle S = \sqrt{s(s-a)(s-b)(s-c)}\;\;,\:s = \frac{a+b+c}{2}$
이하 수학공식카드입니다.
퍼가는 거 막아놓지 않았으니, 다운로드 받아서 쓰세요.



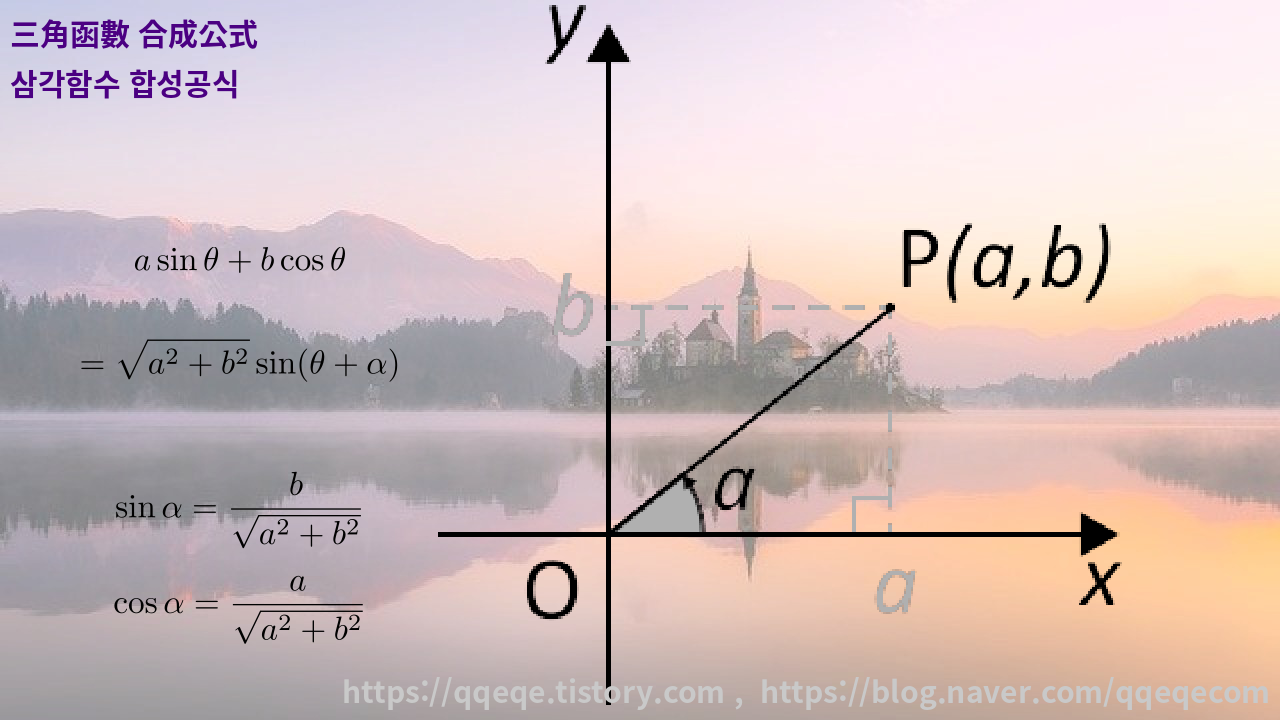





'수학과목' 카테고리의 다른 글
| 중국 고등학교 / Nike함수(耐克函数) (0) | 2022.01.09 |
|---|---|
| 고등학교 적분법 공식 (0) | 2022.01.09 |
| 고등학교 미분법 공식 (0) | 2022.01.09 |
| 삼각함수 공식 2/4 (중국 고2 필수4) (0) | 2022.01.08 |
| 수학에 쓰이는 크고 작다 등등의 중국어 표현 (0) | 2021.11.01 |




댓글